The graph pooling is an operation that perform the down-scaling of a graph by fusioning nodes connected by a common edge. This operation is not identical to the pixel pooling because no regular geometry is available in a graph. It is based on an edge choice critertion based on the properties of the graph (distance, arity of the nodes…).

At any pooling step, the node features are mixed by a function (max, min, mean…) as done usually in regular convolution. The hidden feature must be fusionned too. For example, in the case of cartesian coodinates, a barycenter can be calculated.

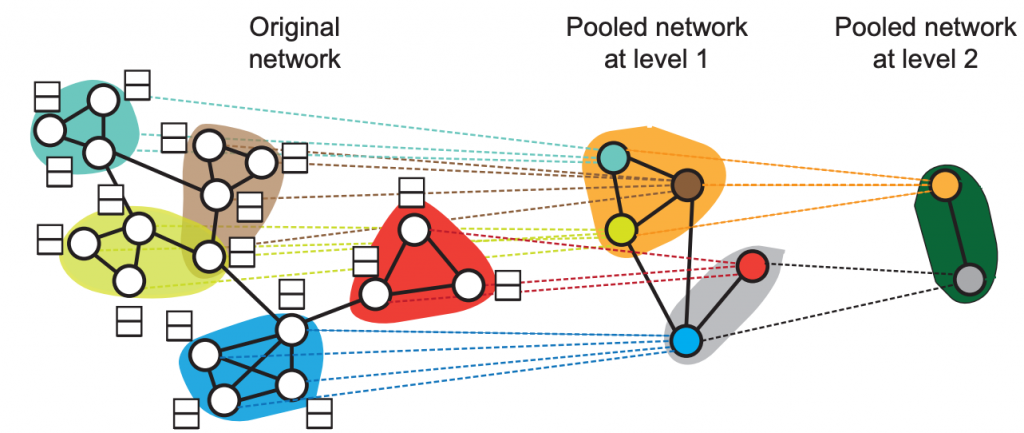
The following figure show the principle of the pooling

The following pseudo-code describes the pooling algorithm

For each edge e in selected_edges(graph):
    x,y=nodes(e)
    n=new_node(graph)
    n.features=pool_function(x,y)
    for t in neighbors(x):
        add_edge(n,t,features(edge(x,t))
    for t in neighbors(y):
        add_edge(n,t,features(edge(y,t))
    remove_edge(graph,e)   
    remove_node(graph,x)
    remove_node(graph,y)

The pool function fusion the two nodes features vectors. It is often a simple function like max, min or mean. The size of the feature vector must be the same for both nodes. Here is a code with the max function

pool_function(node x, node y):
    result=[]
    for i in range(len(features(x)):
        result[i]=max(features(x)[i],features(y)[i])
    return result

The choice for selecting edges can be various. It can be based on the features themselves (for example by defining a distance on the features), or on geometric criterions stored on the nodes outside the features (hiddden features).

The pool function can also modify the hidden features, for example, if some coordinates are stored inside, when merging two nodes, it is a good idea to compute the barycenter coordinates and to add them as hidden features of the new node.

pool_hf_function(node x, node y):
    result=[]
    for i in range(len(hidden_features(x)):
        result[i]=mean(hidden_features(x)[i],hidden_features(y)[i])
    return result

Obviously, this function has to be tailored depending on the exact nature of every field inside the hidden features.